内容来自于《算法》(第4版)
背包、队列和栈
许多基础数据类型都和对象的集合有关。具体来说，数据类型的值就是一组对象的集合，所有的操作都是关于添加、删除或是访问集合中的对象。
泛型，也叫做参数化类型
背包：是一种不支持从中删除元素的集合的数据类型，它的目的就是帮助用例收集元素。迭代的顺序不确定并且与用例无关。使用Bag可以说明元素的处理顺序不重要。
算法表达式求值
E.W.Dijkstra在20世纪60年代发明了一个非常简单的算法，用两个栈（一个用于保存运算符，一个用于保存操作数）完成了这个任务。
表达式由括号、运算符和操作数（数字）组成。根据以下4中情况从左到右逐个将这些实体送入栈处理：
- 将操作数压入操作数栈
- 将运算符压入运算符栈
- 忽略左括号
- 在遇到右括号时，弹出一个运算符，弹出所需数量的操作数，并将运算符和操作数的运算结果压入操作数栈
++i和i++的区别：
- ++i先自增，然后访问i的值
- i++先访问i的值然后自增，
对象游离
Java中的垃圾收集策略是回收所有无法被访问的内存。在对pop()的实现中，被弹出的元素的引用仍然存在于数组中，这个元素实际上已经是一个孤儿了，它永远不会再被访问了，但java的垃圾收集器没法知道这一点，除非该引用被覆盖。即使用例已经不再需要这个元素了，数组中的引用仍然可以让它继续存在。这种情况（保存一个不需要对象的引用）称为游离。避免对象游离很容易，只需要将被弹出的数组元素的值设为null即可，这将覆盖无用的引用并使系统可以在用例使用完被弹出的元素后回收它的内存。
共变（协变）数组
数组的协变性是指：
如果类Base是类Sub的基类，那么Base[]就是Sub[]的基类。
而泛型是不可变的，List
数组的具体化
数组是具体化的，而泛型在运行时是被擦除的。数组在运行时才去判断数组元素的类型约束。 而泛型正好相反，在运行时，泛型的类型信息是会被擦除的，只有编译的时候才会对类型进行强化。
算法分析
近似运行时间
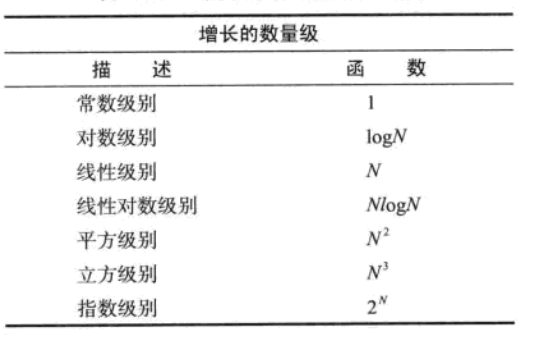
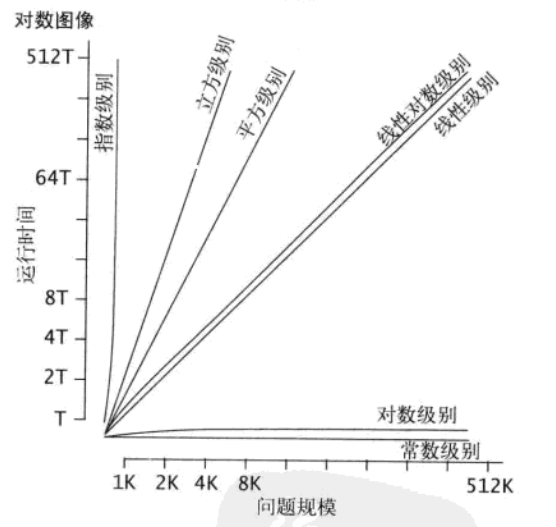
常见的增长数量级函数
使用一个成本模型来评估算法的性质。这个模型定义了所研究的算法中的基本操作。
3-sum的成本模型。在研究3-sum问题的算法时，我们记录的是数组的访问次数（访问数组元素的次数，无论读写）。
对于大多数程序，得到其运行时间的数学模型所需要的步骤如下：
- 确定输入模型，定义问题的规模
- 识别内循环
- 根据内循环中的操作确定成本模型
- 对于给定的输入，判断这些操作的执行频率。这可能需要进行数学分析。
白名单：它的输入模型是白名单的大小N和由标准输入得到的M个整数，假设M»N,内循环是一个while循环中的所有语句，成本模型是比较操作（承自二分查找）。由二分查找的分析我们可以得到对白名单问题的分析，比较次数最多为M(lgN+1)
算法分析中的常见函数
算法分析中的常用的近似函数
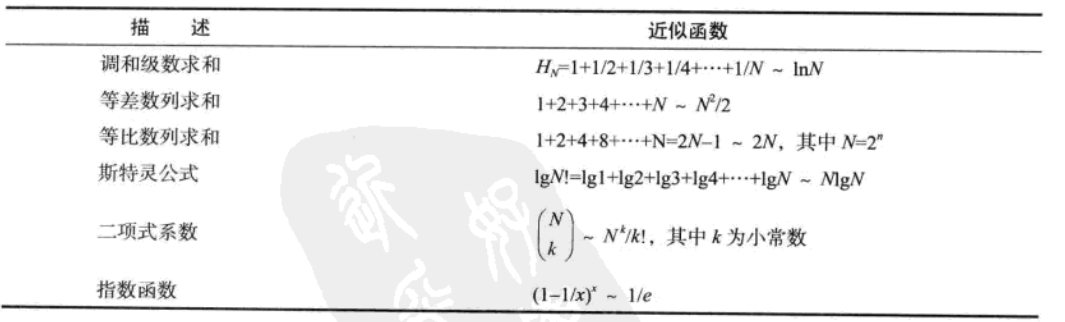
对增长数量级的常见假设的总结
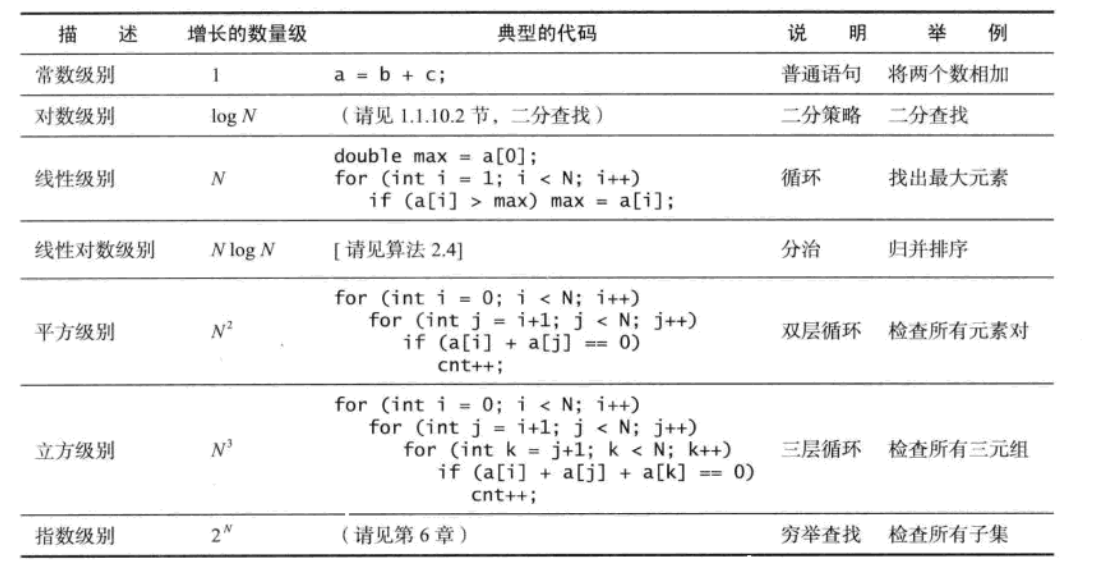
问题规模
