DanWang Blog

算法第4版-排序-希尔排序-归并排序-快速排序

内容来自于《算法》(第4版)

归并排序

希尔排序为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。

希尔排序的思想是是数组中任意间隔为h的元素都是有序的。这样的数组被称为h有序数组。换句换说，一个h有序数组就是h个互相独立的有序数组编织在一起组成的一个数组。

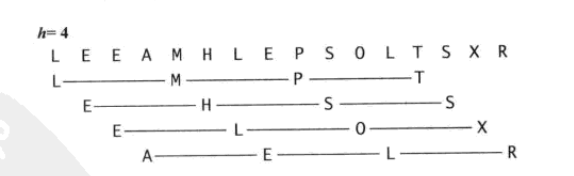
一个h有序数组

在进行排序时，如果h很大，我们就能将元素移动到很远的地方，为实现更小的h有序创造方便。用这种方式，对于任意以1结尾的h序列，我们都能够将数组排序。这就是希尔排序。

实现希尔排序的一种方法是对于每个h，用插入排序将h个子数组独立的排序。但因为子数组时相互独立的，一个更简单的方法是在h-子数组中将每个元素交换到比它大的元素之前去（将比它大的元素向右移动一格）。只需要在插入排序的代码中将移动元素的距离由1改为h即可。这样，希尔排序的实现就转化为了一个类似于插入排序但使用不同增量的过程。

希尔排序更高效的原因是它权衡了子数组的规模和有序性。排序之初，各个子数组都很短，排序之后子数组都是部分有序的，这两种情况都很适合插入排序。子数组部分有序的程度取决于递增序列的选择。

通过提升速度来解决其他方式无法解决的问题是研究算法的设计和性能的主要原因之一。

使用递增序列1,4,13,40,121,364…的希尔排序所需的比较次数不会超出N的若干倍乘以递增序列的长度。

归并排序

归并排序基于归并，即将两个有序的数组归并成一个更大的有序数组。

要将一个数组排序，可以先递归地将它分成两半并分别排序，然后将结果归并起来。你将会看到，归并排序最吸引人的性质是它能够保证将任意长度为N的数组排序所需时间和NlogN成正比，它的主要缺点则是它所需的额外空间和N成正比。

原始归并的抽象方法：

public static void merge(Comparable[] a, int lo,int mid,int hi){
    //将a[lo...mid]和a[mid+1...hi]归并排序
	int i=lo,j=mid+1;
	for(int k=lo;k<=hi;k++) //将a[lo..hi]复制到aux[lo..hi]
	    aux[k]=a[k];
		
	for(int k=lo;k<=hi;k++) //归并回到a[lo..hi]
	    if(i>mid) a[k]=aux[j++];
		else if(j>hi) a[k]=aux[i++];
		else if(less(aux[j],aux[i])) a[k]=aux[j++];
		else a[k]=aux[i++];
}

该方法先将所有元素复制到aux[]中，然后再归并回a[]中。方法在归并时（第二个for循环）进行了4个条件判断，左半边用尽（取右边的元素），右半边用尽（取左半边元素）、右半边当前元素小于左半边当前元素（取右半边元素），右半边当前元素大于等于左半边的当前元素（取左半边元素）。

自顶向下的归并排序

    private static Comparable[] aux;
	
	public static void sort(Comparable[] a){
		aux=new Comparable[a.length];
		sort(a,0,a.length-1);
	}
	
	private static void sort(Comparable[] a, int lo,int hi){
		//将数组a[lo..hi]排序
		if(hi<=lo) return;
		int mid=lo+(hi-lo)/2;
		sort(a,lo,mid);
		sort(a,mid+1,hi);
		merge(a,lo,mid,hi);
	}

自顶向下的归并排序需要的比较次数

对于长度为N的任意数组，自顶向下的归并排序最多需要访问数组6NlogN次。每次归并最多需要访问数组6N次，2N次用来复制，2N次用来将排好序的元素移动回去，另外最多比较2N次。

归并排序所需要的时间和NlogN成正比。我们只需要比遍历整个数组多个对数因子的时间就能将一个庞大的数组排序。可以用归并排序处理百万甚至更大规模的数组，这是插入排序或者选择排序做不到的。归并排序的主要缺点是辅助数组所使用的额外空间和N的大小成正比。

自底向上的归并排序会动词遍历整个数组，根据子数组的大小进行两两归并。子数组的大小sz的初始值为1，每次加倍。最后一个子数组的大小只有在数组大小是sz的偶数倍的时候才会等于sz（否则会比sz）小。

对于长度为N的任意数组，自底向上的归并排序需要1/2NlgN至N此比较，最多访问数组6NlgN次。

当数组长度为2的幂时，自顶向下和自底向上的归并排序所用的比较次数和数组访问次数正好相同。

没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。

归并排序是一种渐进最优的基于比较排序的算法。

归并排序在最坏情况下的比较次数和任意基于比较的排序算法所需的最少比较次数都是~NlgN。

快速排序

快速排序流行的原因是它实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。快速排序引人注目的特点包括它是原地排序（主需要一个很小的辅助栈），且长度为N的数组排序所需的时间和NlgN成正比。另外，快速排序的内循环比大多数排序算法都要短小，这意味着它无论是理论上海市在实际中都要更快。

快速排序是一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立排序。快速排序和归并排序是互补的。归并排序将数组分成两个子数组分别排序，并将有序的子数组归并以将整个数组排序，而快速排序将数组排序的方式则是当两个子数组都有序时整个数组也就自然有序了。在第一种情况中，递归调用发生在处理整个数组之前；在第二种情况中，递归调用发生在处理整个数组之后。在归并排序中，一个数组被等分为两半，在快速排序中，切分的位置取决于数组的内容。

快速排序代码：

	public static void sort(Comparable[] a){
		StdRandom.shuffle(a);//清除对输入的依赖
		sort(a,0,a.length-1);
	}
	
	private static void sort(Comparable[] a, int lo,int hi){
		if(hi<=lo) return ;
		int j=partition(a,lo,hi);
		sort(a,lo,j-1);//将左半部分排序
		sort(a,j+1,hi);//将右半部分排序
	}
	
	private static int partition(Comparable[] a,int lo,int hi){
		//将数组切分为a[lo..i-1] a[i] a[i+1..hi]
		int i=lo,j=hi+1;//左右扫描指针
		Comparable v=a[lo];//切分元素
		while(true){
			//扫描左右，检查扫描是否结束并交换元素
			while(less(a[++i],v)) if(i==hi) break;
			while(less(v,a[--j])) if(j==lo) break;
			if(i>=j) break;
			exch(a,i,j);
		}
		exch(a,lo,j);//将v=a[j]放入正确的位置
		return j;
	}

快速排序递归地将子数组排序，先用partition()方法将a[j]放到合适的位置，然后在递归调用将其他位置的元素排序。

该方法的关键在于切分，这个过程使得数组满足下面三个条件：

切分方法的一般策略是先随意的取a[lo]作为切分元素，即那个将会被排定的元素，然后从数组的左端开始扫描直到找到一个大于等于它的元素，再从数组的右端开始向左扫描直到找到一个小于等于它的元素。这两个元素显然是没有排定的，因此我们交换他们的位置。如此继续，我们就可以保证指针i左侧元素都不大于切分元素，右指针j的右侧元素都不小于切分元素。当两个指针相遇时，我们只需要将切分元素a[lo]和左子数组最右侧的元素a[j]交换然后返回j即可

如果使用一个辅助数组，我们可以很容易的实现切分，但将切分后的数组复制回去的开销也许会使我们得不偿失。如果将空数组创建在递归的切分方法中，这回大大降低排序的速度。

终止循环需要格外小心，正确地检测指针是否越界需要一点技巧，常见的错误时没有考虑到数组中可能包含和切分元素的值相同的其他元素。

左侧扫描最好是在遇到大于等于切分元素值的元素时停下，右侧扫描是遇到小于等于切分元素值的元素时停下，尽管这可能会不必要地将一些等值的元素交换，但在某些典型应用中，它能够避免算法的运行时间变为平方级别。

快速排序的一个优点是内循环的简洁性。另一个速度优势在于比较次数少。

将长度为N的无重复数组排序，快速排序平均需要~2NlnN次比较（以及1/6的交换）。

快速排序有很多优点，它的基本实现有一个潜在的缺点，在切分不平衡时，这个程序可能会极为低效。例如，第一次从最小的元素切分，第二次从第二小的元素切分，这样的话，每次调用只会移除一个元素，这会导致一个大子数组需要切分很多次，我们要在快速排序前将数组随机排序的主要原因就是要避免这种情况，能够使得产生糟糕的切分的可能性降到极低，

快速排序最多需要N*N/2次比较，但随机打乱数组能够预防这种情况。

快速排序的算法改进

切换到插入排序

和大多数递归排序算法一样，改进快速排序性能的一个简单办法基于以下两点：

因此在排序小数组时应该切换到插入排序。

三取样切分

改进快速排序性能的第二个办法是使用子数组的一小部分元素的中位数来切分数组。这样做得到的切分更高，但是需要计算中位数，取样大小设为3并用大小居中的元素切分的效果最好。

熵最优的排序

实际应用中经常会出现含有大量重复元素的数组。一个元素全部重复的子数组就不需要排序了，但我们的算法还会继续切分为更小的数组。一个简单的想法是将数组三切分，分别对应于小于、等于和大于切分元素的数组元素。

Dijkstra的解法，从左到右遍历数组一次，维护一个指针lt使得a[lo..lt-1]中的元素都小于v，一个指针gt使得a[gt+1..hi]中的元素都大于v，一个指针i使得a[lt..i-1]中的元素都等于v，a[i..gt]中的元素还未确定。一开始i=lo，使用下面方法来处理：

这些操作都会保证数组元素不变且缩小gt-i的值（这样循环才会结束）。另外，除非和切分元素相等，其他元素都会被交换。