内容来自于《机器学习》
间隔与支持向量
在样本空间中,划分超平面可通过如下方程来描述:
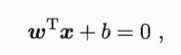
其中w为法向量,决定了超平面的方面;b为位移项,决定了超平面与原点之间的距离。显然,划分超平面可被法向量和位移b确定,记为(w,b)。
样本空间中任意点x到超平面(w,b)的距离可写为:
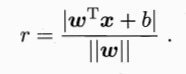
假设超平面(w,b)能够将训练样本正确分类,对于D中的(xi,yi),若yi=+1,有wTxi+b>=+!;若yi=-1,有wTxi+b《0;
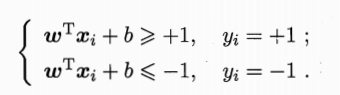
如图所示:
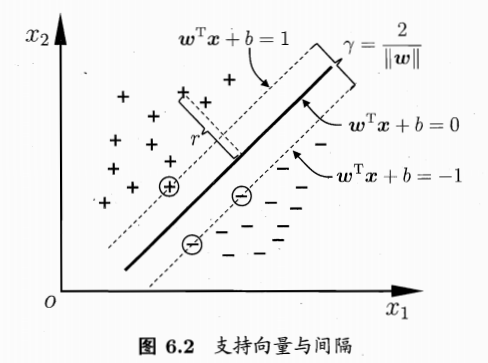
距离超平面最近的这几个训练样本点使得上述等式成立,它们被称为支持向量,两个异类支持向量到超平面的距离之和为:
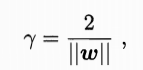
它被称为间隔。
| 要找到具有最大间隔的划分超平面,需要最大化 | w | ^-1, |
即:
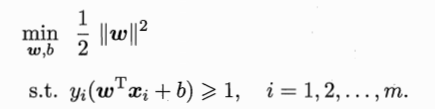
这就是支持向量机的基本型
对偶问题
希望求解上述公式来得到大间隔划分超平面对应的模型:

其中w和b是模型参数。
训练完成之后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关、
核函数
有些问题不是线性可分的,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。
只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。事实上,对于一个半正定矩阵,总能找到一个与之对应的映射。换言之,任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间”(Reproducing Kernel Hilbert Space,RKHS)的特征空间。


软间隔与正则化
现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分,即便恰好找到了 某个核函数使训练集在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。
缓解该问题的一个方法是允许支持向量机在一些样本上出错。为此,引入“软间隔”:
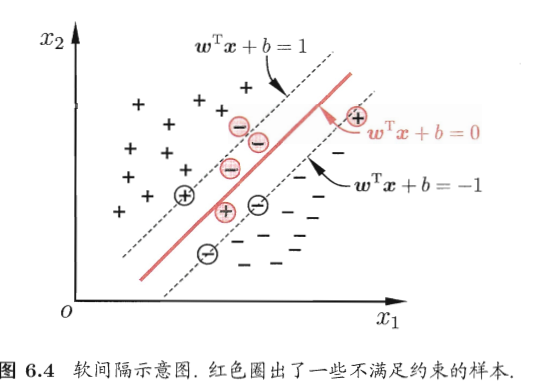
之前介绍的支持向量机要求所有样本都满足条件,即所有样本都必须划分正确,这成为硬间隔。软间隔允许某些样本不满足约束
在最大化间隔的同时,不满足约束的样本应尽可能少,优化目标为:
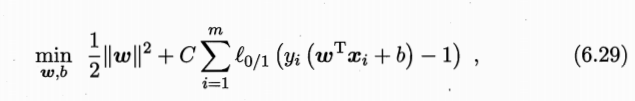
其中C>0是一个常数,L0/1是“0/1损失函数”
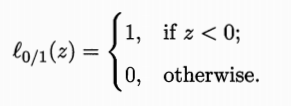
但是该损失函数非凸、非连续、数学性质不太好,通常使用其他一些函数来替代这个损失函数,称为“替代损失”.
三种常用的替代损失函数:
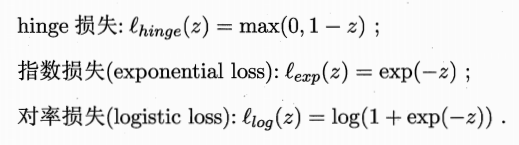
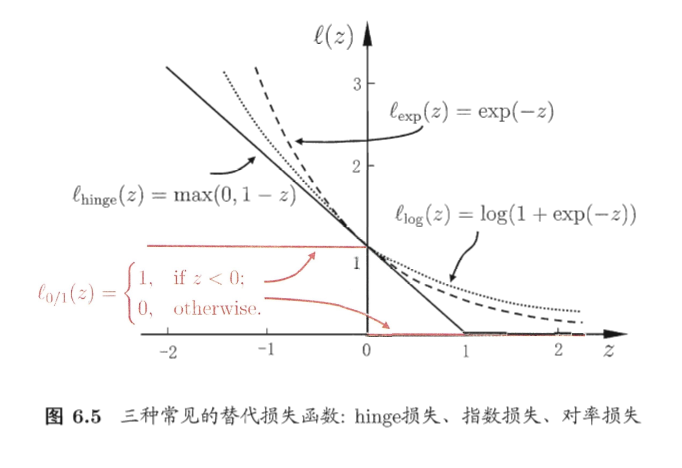
最后形成了常用的软间隔支持向量机。
Lp范数
支持向量回归
支持向量回归假设我们能容忍f(x)与y之间最多有epsilon的偏差,仅当两者之间的差别绝对值大于epsilon时才计算损失。
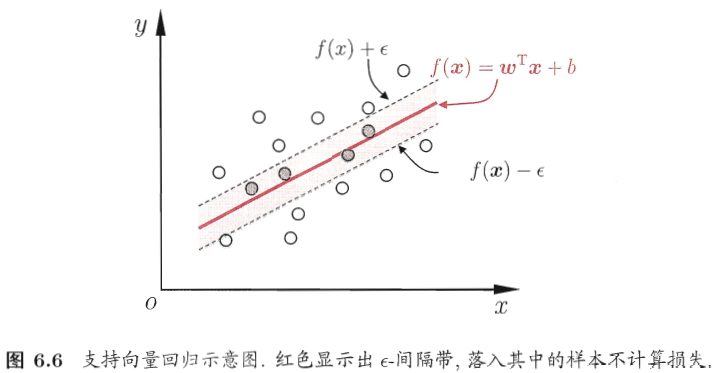
核方法
给定训练样本,若不考虑偏移项b,则无论SVM还是SVR,学得的模型总能表示成核函数的线性组合。

表示定理对损失函数没有限制,对正则化项仅仅要求单调递增,甚至不要求正则化项是凸函数意味着对月一般的损失函数和正则化项,优化问题6.57的最优解都可以表示为核函数的线性组合。
人们发展处一系列基于核函数的学习方法,统称为核方法,最常见的,是通过核化(引入核函数)来将线性学习器拓展为非线性学习器。
 DanWang Blog
DanWang Blog