DanWang Blog

集成学习

内容来自于《机器学习》

个体与集成

集成学习通过构建并结合多个学习器来完成学习任务，有时也被成为多分类器系统（multi-classifier system）、基于委员会的学习(committee-based learning)等。

集成学习的一般结构为，先产生一组个体学习器，再用某种策略将它们结合起来。个体学习器通常由一个现有的学习算法从训练数据产生，此时集成中只包含同种类型的个体学习器，例如决策树集成中全是决策树，这样的集成是同质的。同质集成中的个人学习器亦称为基学习器，相应的学习算法称为基学习算法。集成也可以包含不同类型的个体学习器，这样的集成是异质的。异质集成中的个体学习器由不同的学习算法生成，这时就不再有基学习算法。相应的，个体学习器不称为基学习器，常称为组件学习器或者直接称为个体学习器。

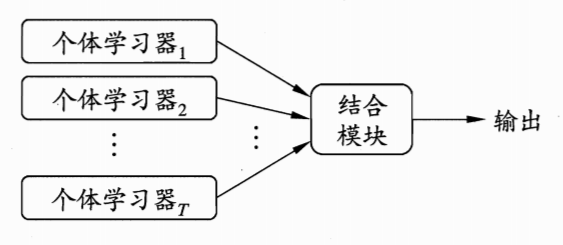
集成学习通过将多个学习器进行结合，常课获得比单一学习器显著优越的泛化性能。这对弱学习器尤为明显，因此集成学习的很多理论都是针对弱学习器进行的。而基学习器有时候也被直接称为弱学习器，但需要注意的是，虽然从理论上来说，使用弱学习器集成足以获得好的性能，但在实践中出于种种考虑，例如希望使用较少的个体学习器，或是重用关于常见学习器的一些经验等，人们往往会使用比较强的学习器。

要获得好的集成，个体学习器应该“好而不同”，即个体学习器要有一定的准确性，即学习器不能太坏，并且要有多样性，即学习器间具有差异。

个体学习器的准确性和多样性本身存在冲突，一般的，准确性很高之后，要增加多样性就需要牺牲准确性，事实上，如何产生并结合好而不同的个体学习器，恰是集成学习研究的核心。

根据个体学习器的生成方式，目前的集成学习方法大致可分为两类，即个体学习器间存在强依赖关系，必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系，可同时生成的并行化方法；前者的代表是Boosting，后者的代表是Bagging和随机森林（Random Forest）。

Boosting

Boosting 是一族可将弱学习器提升为强学习器的算法，这族算法的工作机制类似：先从初始训练集训练出一个基学习器，在根据基学习器的表现对训练样本分布进行调整，使得闲钱学习器做错的训练样本在后续收到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权结合。

Boosting族算法最著名的代表是AdaBoost,算法描述如下：

其中，yi属于{-1，+1},f是真实函数

AdaBoost有多种推导方式，比较容易理解的是基于加性模型（additive model）即基于学习器的线性组合：

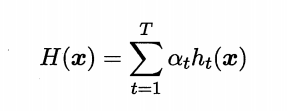
来最小化指数损失函数：

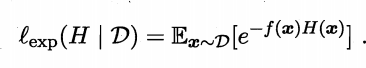
若指数损失函数最小化，则分类错误率也将最小化，这说明指数损失函数是分类任务原本0/1损失函数的一致的替代损失函数。由于这个替代函数有更好的数学性质，因此用它替代0/1损失函数作为优化目标、

Boosting 算法要求基学习器能对特定的数据分布进行学习，这可通过重赋权法 实施，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重。对无法接受带权样本的基学习算法，则可通过重采样法来处理，即在每一轮学习中，根据样本分布对训练集重新进行采样，在用重采样而得的样本集对基学习器进行训练。一般而言，这两种做法没有显著的优劣差别。需要注意的是，Boosting算法在训练的每一轮都要检查当前生成的基学习器是否满足基本条件，一旦条件不满足，则当前基学习器即被抛弃，且学习过程停止，在此种情形下，初始设置的学习轮数也许还远未达到，可能导致最终集成中只包含很少的基学习器而性能不佳，若采用重采样法，则可获得重启动的机会，避免训练过程过早停止，即在抛弃不满足条件的当前学习器之后，可根据当前分布重新对训练样本进行采样，再基于新的采样结果重新训练处基学习器，从而使得学习过程可以持续预设的T论完成。

从偏差–方差分解的角度看，Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当若的学习器构建出很强的集成。

Bagging与随机森林

遇得到泛化性能强的集成，集成中的个体学习器应尽可能相互独立，虽然独立在现实任务中无法做到，但可以设法使几学期尽可能具有较大的差异。给定一个训练数据集，一种可能的做法是对训练样本进行采样，产生若干不同的自己，再从每个数据自己种训练处一个基学习器，这样，由于训练数据不同，我们获得的基学习器可能具有比较大的差异，然而，为获得好的集成，我们同时还希望个体学习器不能太差。如果采样出的每个子集都完全不同，则每个基学习器都只用到了一小部分训练数据，甚至不足以进行有效学习，这显然无法确保产生出比较好的基学习器。为了解决这个问题，我们可考虑使用相互有交叠的采样自子集。

Bagging

Bagging 是并行式集成学习方法最著名的代表，从名字即可看出，它直接基于自助采样法，给定包含m个样本的数据集，我们先随机取出一个样本放入采样集中，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中这样，经过m次随机采样操作，我们得到含m个样本的采样集，初始训练集中有的样本在采样集中多次出现，有的则从未出现。

我们可采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合。这就是Bagging的基本流程。在对预测输出进行结合时，Bagging通常对分类任务使用简单投票法，对回归任务使用简单平均法。若分类预测时出现两个类收到同样票数的情况，则最简单的做法是随机选择一个，也可以进一步考察学习器投票的置信度来确定最终胜者，

假定基学习器的计算复杂度为O(m)，则Bagging的复杂度大致为T(O(m)+O(s))，考虑到采样与投票/平均过程的复杂度O(s)很小，而T通常是一个不太大的常数，因此，训练一个Bagging集成与直接使用基学习算法训练一个学习器的复杂度同阶，这说明Bagging是一个很搞笑的集成学习算法，另外，与标准AdaBoost只适用于二分类任务不同，Bagging能不经修改地用于多分类、回归等任务。

自助采样过程还给Bagging带来另一个优点：由于每个基学习器只使用了初始训练集中约63.2%的样本，剩下的样本可以用作验证集来对泛化性能进行包外估计（out-of-bag estimate）。为此徐记录每个基学习器使用的训练样本。

令Hoob(x)表示对样本x的包外预测，即仅考虑那些未使用x训练的基学习器在x上的预测，有

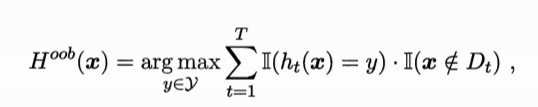
则Bagging泛化误差的包外估计为：

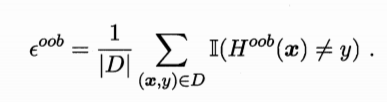
包外样本还有许多其它用途，例如当继续基学习器是决策树时，可使用包外样本来辅助剪枝，或者用于估计决策树中各结点 的后验概率以辅助对零训练样本结点的处理，当基学习器是神经网络时，可使用包外样本来辅助早起停止以减小过拟合风险。

从偏差-方差分解的角度看，Bagging主要关注降低方差，因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。

随机森林

随机森林（Random Forest简称RF）是Bagging的一个扩展变体，RF在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。具体来说，传统决策树在选择划分属性时是在当前结点的属性集合（假定有d个属性）中选择一个最优属性；而在RF中，对基决策树的每个结点，先从该节点的属性集合中随机选择一个包含k个属性的子集。然后再从这个子集中选择一个最优属性用于划分这里的参数k控制了随机性的引入程度。若令k=d，则基决策树的构建与传统决策树相同，若令k=1，则是随机选择一个属性用于划分，一般情况下，推荐值k=log2d。

随机森林简单、容易实现、计算开销小，令人惊奇的是，它在很多现实任务中展现出强大的性能，被誉为代表集成学习技术水平的方法。可以看出，随机森林对Bagging只做了小改动，但是与Bagging中基学习器的多样性，仅通过样本扰动（通过对初始训练集采样）而来不同，随机森林中基学习器的多样性不仅来自样本扰动，还来自属性扰动，这就使得最终集成的泛化性能课通过个体学习器之间的差异度的增加进一步提升。

随机森林的收敛性与Bagging相似。随机森林的起始性能往往相对较差，特别是在集成中只包含一个基学习器时，这很容易理解，因为通过引入属性扰动，随机森林中个体学习器的性能往往有所降低。然而，随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差。值得一提的是，随机森林的训练效率常常优于Bagging，因为在个体决策树的构建过程中，Bagging使用的是确定性决策树，在选择划分属性时要对结点的所有属性进行考察，而随机森林使用的随机型，决策树只需考察一个属性子集。

集合策略

学习器的集合可能会从三个方面带来好处：1. 首先从统计的方面来看，由于学习任务的假设空间往往很大，可能有多个假设在训练集上达到同等性能，此时若使用但学习器可能因误选而导致泛化性能不佳，结合多个学习器可以减小这一风险。2. 从计算的方面来看，学习算法往往会陷入局部极小，有的局部极小点所对应的泛化性能可能很糟糕，而通过多次运行之后进行结合，可降低陷入糟糕局部极小点的风险。3. 从表示的方面来看，某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中，此时若使用但学习期则肯定无效。而通过结合多个学习器，由于相应的假设控件有所扩大，有可能学得更好的近似。

假定集成包含T个基学习器{h1,h2,…,hT},其中hi在示例x上的输出为hi(x)。对hi进行结合的常见策略如下：

平均法： +简单平均法 +加权平均法

投票法：

学习法

个体学习器称为初学习器，用于结合的学习器称为次级学习器或者元学习器。

多样性

个体学习器准确性越高、多样性越大，则集成越好。

多样性度量是用于度量集成中个体分类器的多样性，即估算个体学习器的多样化程度，典型做法是考了个体分类器的两两相似/不相似性。

常见的多样性度量：

多样性增强：