内容来自于《机器学习》

基础知识

计算学习理论 computational learning theory 研究的是关于通过计算来进行学习的理论

独立同分布 independent and identically distributed 简称i.i.d.

经验误差与繁华误差的逼近程度。若h在数据集D上的经验误差为0，则称h与D一致，否则称其与D不一致。对于任意两个映射h1,h2∈X->Y，可通过其 不合 disagreement 来度量它们之间的差别。

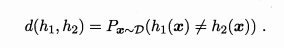
• Jensen 不等式：

• Hoeffding不等式：

• McDiarmid不等式：

PAC学习

计算学习理论中最基本的是概率近似正确 Probably Approximately Correct，简称PAC，学习理论。

令c表示概念 concept，这是从样本空间X到标记空间Y的映射，它决定实例x的真实标记y，若对任何样例（x,y）有c(x)=y成立，则称c为目标概念，所有我们希望学得的目标概念所构成的集合成为概念类 concept class，用符号C表示。

给定学习算法，它所考虑的所有可能概念的集合成为假设空间hypothesis space，用符号H表示。

希望以较大的把握学得比较好的模型，也就是说，以较大的概率学得误差满足预设上限的模型，这就是概率 近似正确的含义。

PAC辨识 PAC Identify

PAC可学习 PAC Learnable

PAC 学习算法 PAC Learning Algorithm

样本复杂度 Sample Complexity

恰PAC可学习 properly PAC learnable

有限、无限假设空间

有限假设空间

VC维

VC维 Vapnik-Chervonenkis dimension

增长函数 growth function

对分 dichotomy

打散 shattering

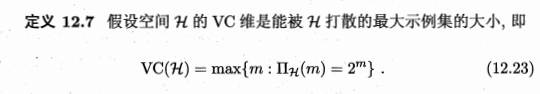
VC(H)=d表明存在大小为d的示例集能被假设空间H打散。VC维的定义与数据分布D无关，因此在数据分布未知时仍能计算出假设空间H的VC维。

通常这样来计算H的VC维：若存在大小为d的示例集能被H打散，但不存在任何大小为d+1的示例集能被H打散，则H的VC维是d。

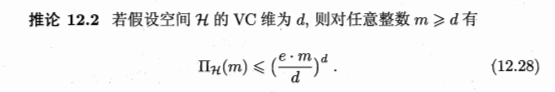
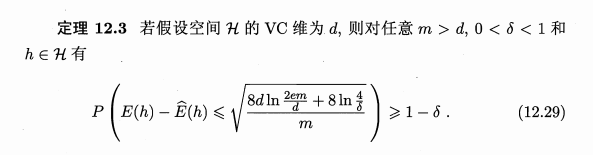
Rademacher复杂度

基于VC维的泛化误差界是分布无关、数据独立的，也就是对任何数据分布都成立，这使得基于VC维的可学习性分析结果具有一定的普适性。但从另一方面来说，由于没有考虑数据自身，基于VC维得到的泛化误差界通常比较松，对那些与学习问题的典型情况相差甚远的较坏分布来说尤其如此。

Rademacher复杂度是另一种刻画假设空间复杂度的途径，在一定程度上考虑了数据分布。

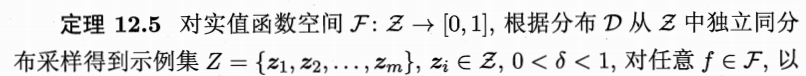
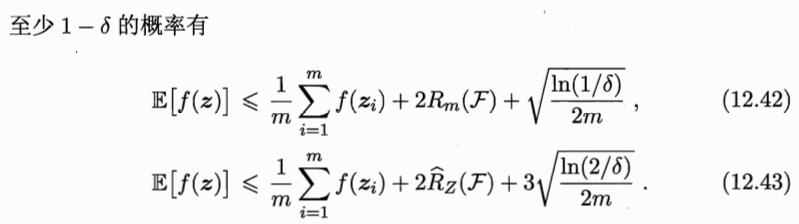
稳定性

无论是基于VC维还是Rademacher复杂度来推导泛化误差界，所得到的结果均与具体学习算法无关，对所有的学习算法适用。这使得人们能够脱离具体学习算法的设计来考虑学习问题本身的性质，但在另一方面，若希望获得与算法有关的分析结果，则需另辟蹊径，稳定性分析是一个值得关注的方面